Math 136 - Week 1
Chapter 1 - Vectors in Euclidean Space
1.1 Vector Addition and Scalar Multiplication
Instead of points, we work with vectors.
The set
Two vectors
In other words, they are said to be equal if the vectors are both in the same space (
For example,
And,
But,
Just because you are working in
Geometrically, a vector in
Let
Addition,
In linear algebra, a scalar is just a number in
Subtraction is just defined as the addition of a negative. When we write
For
Add
Geometrically, We can express it as:
For
a linear combination of
This definition IS EXTREMELY IMPORTANT!!!!
If
Proofs:
Let
Since
Let
As desired.
Let
As desired.
As desired.
As desired.
As desired.
As desired.
1.1 - Problems
- Compute the following linear combinations.
.
Solution:
.
Solution:
\displaystyle\frac{1}{3}\begin{bmatrix}3 \ 1 \ -2\end{bmatrix} - \begin{bmatrix}4 \ \frac{1}{2} \-\frac{2}{3}\end{bmatrix} &= \begin{bmatrix}1 \ \frac{1}{3} \ -\frac{2}{3}\end{bmatrix} + \begin{bmatrix}-4 \ -\frac{1}{2} \\frac{2}{3}\end{bmatrix} \
&= \begin{bmatrix} -3 \ -\frac{1}{6} \ 0
\end{bmatrix}
\end{aligned} \Solution: \sqrt{ 2 }\begin{bmatrix}\sqrt{ 2 } \ 0 \ \sqrt{ 2 }\end{bmatrix} + \displaystyle\frac{2}{3}\begin{bmatrix}6 \ 0 \ 0 \end{bmatrix} &= \begin{bmatrix} 2 \ 0 \ 2\end{bmatrix} + \begin{bmatrix}4 \ 0 \ 0 \end{bmatrix} \
&= \begin{bmatrix}
6 \ 0 \ 2
\end{bmatrix}
\endSolution: (a+b) \begin{bmatrix} 1 \ 1 \ -1\end{bmatrix} + (-a+b) \begin{bmatrix} 1 \ 2 \ -3\end{bmatrix} + (-a+2b) \begin{bmatrix} -1 \ -1 \ 2\end{bmatrix} &= \begin{bmatrix} (a+b) \ (a+b) \ -(a+b)\end{bmatrix} + \begin{bmatrix} (-a+b) \ 2(-a+b) \ -3(-a+b)\end{bmatrix} + \begin{bmatrix} -(-a+2b) \ -(-a+2b) \ 2(-a+2b)\end{bmatrix} \
&= \begin{bmatrix} a-a+a+b+b-2b \ a -2a+a+b+2b-2b \ -a+3a-2a-b-3b+4b\end{bmatrix} \
&= \begin{bmatrix}
a \ b \ 0
\end{bmatrix}
\end.
Solution:
2\vec{x} + 2\vec{v} &= 4\vec{x} \
2\vec{x} + 2(\vec{-x}) + 2\vec{v} &= 4\vec{x} + 2(-\vec{x}) && \text{by V5 and addition} \
2(\vec{x} + (-\vec{x})) + 2\vec{v} &= 2(2\vec{x} + (-\vec{x})) && \text{by V9} \
2(\vec{0}) + 2\vec{v} &= 2(\vec{x}) && \text{by V5 and addition of vectors}\
\vec{0} + 2\vec{v} &= 2\vec{x} && \text{by scalar multiplication} \
2\vec{v}\left( \frac{1}{2} \right)&=2\vec{x}\left( \frac{1}{2} \right) && \text{by V4} \
1\vec{v} &=1\vec{x} && \text{by V7} \
\vec{x} &= \vec{v} && \text{by V10}
\endSolution: \vec{x} + 2\vec{v} &= \vec{v} + (-\vec{x}) \
\vec{x} + \vec{x} + 2\vec{v} + 2(-\vec{v}) &= \vec{v} + 2(-\vec{v}) + -\vec{x} + \vec{x} \
2\vec{x} + 2(\vec{v} + (-\vec{v})) &= \vec{v} + (-2\vec{v}) + \vec{0} && \text{by vector addition, V9, V5} \
2\vec{x} + 2(\vec{0}) &= (-\vec{v}) && \text{by V5, vector addition, V4} \
2\vec{x} + \vec{0} &= (-\vec{v}) && \text{by scalar multiplication} \
2\vec{x} \left( \frac{1}{2} \right) &= (-\vec{v})\left( \frac{1}{2} \right) && \text{by V4} \
1\vec{x} &= \left( -\frac{1}{2} \right) (\vec{v}) && \text{by V7} \
\vec{x} &= \left( -\frac{1}{2} \right)(\vec{v}) && \text{by V10}
\end - Looking at the area of the parallelogram formed by the parallelogram rule for addition on
. - Calculate each of the following and show the result geometrically. Find the area of each parallelogram formed by the parallelogram rule for addition.
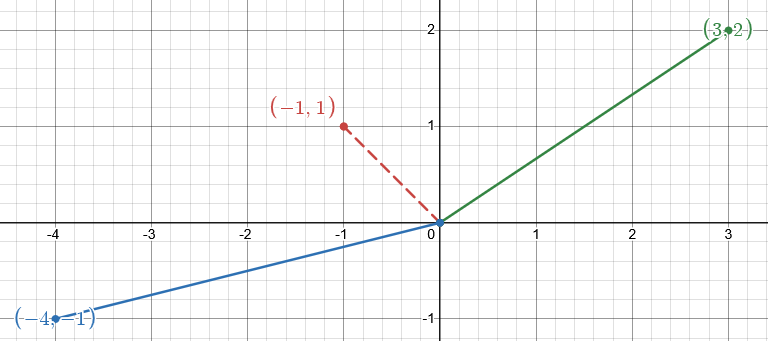
Solution:
2..
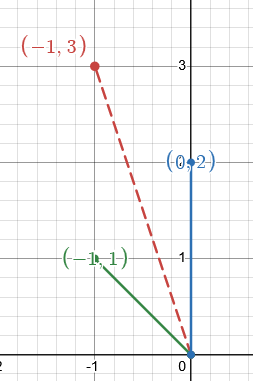
Solution:
- What condition must be placed on
and to ensure that the parallelogram has non-zero area?
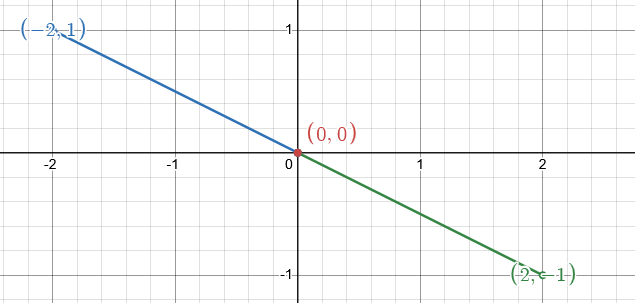
Solution:and geometrically, can't be on the same line together. - Create two more pairs
that form a parallelogram with non-zero area. Find the area of each parallelogram.
Solution:
Area:
Area:
- Find a general formula for the area of the parallelogram determined by
. Prove that your formula is correct.
Solution:
Let.
Area =
- Calculate each of the following and show the result geometrically. Find the area of each parallelogram formed by the parallelogram rule for addition.